Elementos básicos de la Estadística
Para poder recopilar adecuadamente los datos en un estudio estadístico se debe conocer la poblacion objeto de estudio, por medio de una muestra representativa. se llama poblacion al total de sujetos observables y muestra a la "parte representativa" de dicha población.
al efecturar el estudio de una población, éste se centra en ciertas caracteristicas o variables que son importantes para dicho estudio; así, una variable es una característica de los sujetos de la población que puede tomar cualquiera de los valores de un conjunto y que se evalúa por medio de una muestra.
las variables pueden ser continuas o discretas.
Variable continua es aquélla que puede tomar cualquier valor de un conjunto. variable discreta es aquélla que tan sólo puede tomar como valores unidades enteras. si una variable sólo puede tomar un valor recibe el nombre de constante.
los métodos estadísticos comprenden el análisis e interpretación de números, ventas mensuales, calificaciones de exámenes, números de partes defectuosas, porcentaje de respuestas correctas a un cuestionario, años de servicio, tiempo de terminación, etc. a tales números se les conoce como datos
Operación con conjuntos
La Teoría de Conjuntos es una teoría matemática, que estudia básicamente a un cierto tipo de objetos llamados conjuntos y algunas veces, a otros objetos denominados no conjuntos, así como a los problemas relacionados con estos.
El concepto de conjunto es intuitivo y se podría definir como una "agrupación bien definida de objetos no repetidos y no ordenados"; así, se puede hablar de un conjunto de personas, ciudades, gafas, lapiceros o del conjunto de objetos que hay en un momento dado encima de una mesa. Un conjunto está bien definido si se sabe si un determinado elemento pertenece o no al conjunto. El conjunto de los bolígrafos azules está bien definido, porque a la vista de un bolígrafo se puede saber si es azul o no
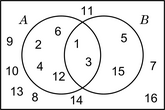
Diagrama de ven
 |
| Diagramas de Venn que corresponden respectivamente a las relaciones topológicas de intersección, inclusión y disyunción entre dos conjuntos |